Tears and Laughters --- my CSC165 studying process.

Saturday, February 26, 2011

Some precious quotes!

http://www.youtube.com/watch?v=xfq_A8nXMsQ&feature=related

Artist(Band): Baz Luhrmann

Ladies and Gentlemen of the class of '97. Wear sunscreen.
If I could offer you one tip for the future, sunscreen
would be it. The
long-term benefits of sunscreen have been proved by
scientists whereas the
rest of my advice has no basis more reliable than my
own meandering
experience... I will dispense this advice now

Enjoy the power and beauty of your youth; oh,
nevermind, you will not
understand the power and beauty of your youth until
they've faded. But trust
me, in 20 years you'll look back at photos of yourself
and recall in a way
you can't grasp now, how much possibility lay before
you and how fabulous
you really looked. You are NOT as fat as you imagine.

Don't worry about the future; or worry, but know that
worrying is as
effective as trying to solve an algebra equation by
chewing bubblegum. The
real toubles in life are apt to be things that never
crossed your worried
mind; the kind that blindside you at 4pm on some idle
Tuesday

Do one thing everyday that scares you.

Sing.

Don't be reckless with other people's hearts. Don't
put up with people who
are reckless with your's.

Floss.

Don't waste your time on jealousy; sometimes you're
ahead, sometimes you're
behind. The race is long, and in the end, it's only with
yourself.

Remember compliments you receive. Forget the
insults. If you suceed in doing
this, tell me how.

Keep your old love letters. Throw away your old bank
statements.

Stretch.

Don't feel guilty if you don't know what you want to do
with your life.
The most interesting people I know didn't know at 22
what they wanted to do
with their lives; some of the most interesting 40 year
olds I know still
don't.

Get plenty of calcium.

Be kind to your knees, you'll miss them when they're
gone.

Maybe you'll marry, maybe you won't. Maybe you'll
have children, maybe you
won't. Maybe you'll divorce at 40. Maybe you'll dance
the funky chicken on
your 75th wedding anniversary. Whatever you do,
don't congratulate
yourself too much or berate yourself either - your
choices are half chance,
so are everybody else's.

Enjoy your body, use it every way you can... don't be
afraid of it, or what
other people think of it... it's the greatest instrument
you'll ever own.

Dance... even if you have nowhere to do it but in
your own living room.

Read the directions, even if you don't follow them.

Do NOT read beauty magazines they will only make
you feel UGLY.

CHORUS
Brother and sister together we'll make it through.
Someday your spirit will take you and guide you there.
I know you've been hurting, but I've been waiting to be there for you.
And I'll be there just helping you out whenever I can.

Get to know your parents, you never know when they
might be gone for good.
Be nice to your siblings; they're your best link to your
past and the
people most likely to stick with you in the future

Understand that friends come and go, but for the
precious few you should
hold on. Work hard to bridge the gaps in geography
and lifestyle because the
older you get, the more you need the people you knew
when you were young.

Live in New York City once, but leave before it makes
you hard. Live in
Northern California once, but leave before it makes
you soft.

Travel.

Accept certain inalienable truths. Prices will rise,
Politicians will
philander, you too will get old. And when you do, you'll
fantasize that when
you were young, prices were reasonable, politicians
were noble, and children
respected their elders.

Respect your elders.

Don't expect anyone else to support you. Maybe
you have a trust fund,
maybe you'll have a wealthy spouse; but you never
know when either one might
run out.

Don't mess too much with your hair, or by the time you're
40, it will look 85.

Be careful whose advice you buy, but, be patient with
those who supply it.
Advice is a form of nostalgia; dispensing it is a way of
fishing the past
from the disposal, wiping it off, painting over the ugly
parts, and
recycling it for more than it's worth.

But trust me on the sunscreen.

CHORUS

Everybody's free. Everybody's free.

Monday, December 6, 2010

A reflection on the process of taking csc165.

Dear all,

Hope everyone is having a pleasant holiday session. Before the end of this course, I'd like to share my experience of taking csc165.

csc165 is one of the six courses that I am taking during this semester. I would say, it's a lot of fun to spend 3 hour going to Danny's lecture every week discussing and exploring some new and interesting math problems. I think one of the greatest ideas about csc165 is that we have a grading system which is very encouraging for students to persist in this course. 3 assignments followed up by 3 tests, and 2 tutorials between every 2 tests. You final marks will be largely and mostly depend on your performance during the study. And the highest mark will have the most proportion. Students won't be too stressed out over the failure of one assignment or a test. In stead, they will try to strive for the best next time. Besides, the slog idea is fantastic! It's a brand-new experience to learn through being a blogger, which is really cool!

The best part of the slog idea for me is that it really allows me the chance to sit down and do some research about some difficult problems. Only if you really try hard to think over those problems which seem so easy at the first sight will you start to really learn something by yourself. Besides, writing blogs is an amazing idea to trace the problems and mistakes I made during the study. The problems will be so ambiguous unless they are written down as an assay. Setting down the problems and explaining the problems help to understant them better.
One of the most important thing I learn from this semester is : No matter how easy or how hard the tasks seem like, procrastination will ruin everything and get you to pay emotionally and mentally for the cost, while starting earlier and working harder will alway help you solve all kind of difficult problems. Sometimes, you just don't believe yourself. The fear of difficulty will get in your way of making things happen. Never lose you faith of your own ability.

Just as the famous quote''Man propose it, God dispose it.'' When you are really trying hard to abtain something you want, you try so hard that the whole world will revolve around you to assist you achieving the goal. The only enemy is not anyone or anything else, it lies in yourself only. The laziness, fear will take control of you when you don't have faith in yourself.

Never doubt yourself, even for a second, never!

This is what I learned from this semester's experience of taking 6 courses, and also taking csc165. It was such a great experience to have known so many classmates, professors, and TAs. I start to really understand what university is offering me -- a chance to get to know the best, and then bring out the best of yourself. Wish everyone great luck on the finals and a Merry Christmas!

Sincerely,
L.gal

Tuesday, November 30, 2010

Why is there more irrational numbers than rational numbers.

why are there far more real number than natural numbers? Why are there far more irrational numbers than rational numbers?
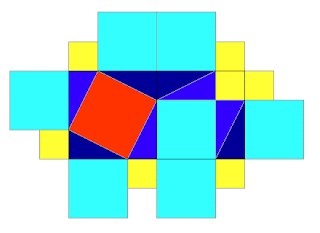
As shown in the graph above, it's called a consequence of the Pythagorean theorem: The length of the diagonal of a square is the square root of two times its side. The length of the square is a rational number while the length of diagonal is irrational. While we can just keep getting the 1/2 of the existing square to get infinitely many rational numbers, these natural numbers are countably many. But the number of irrationals are far more than the rationals, which is illustrated by the cardinality of the rationals and irrationals. |R\Q| >|Q|.

Now here is a trick to show why there are more irrationals than rationals.
We do this by trying to list all the real numbers in the interval (0,1).

First, because each of the rational numbers can be associated with a natural number by listing there like below.

In this way, each number is followed by its negative version, except zero, which doesn't have a different negative version. he fractions, if considered as improper fractions, are ordered by the sum of the numerator and denominator, starting with the fraction with the largest numerator: thus, we go through 4/1, 3/2, 2/3,1/5 in order. (Earlier, 2/2 was omitted, since that equals 1, which is already on the list.)
N Q
1 1/1
2 -1
3 2/1
4 -2/1
5 1/2
6 -1/2
7 3
8 -3
9 1/3
10 -1/3
11 4
12 -4

... ...

Then we can use all the natural numbers to list all the rational numbers. We have |Q| = |N|

Now we are trying to show there are more irrational number than rationals by trying to list all the irrationals by natural numbers.

.27231364585...
.40861132064...
.01678396536...
.81171944218...
.82122547689...
.17218943291...

...
We are trying to list all the real numbers by associating each with a natural number. But it seems there are always at least 1 more irrational number than all the rational numbers that we can list. Assume we listed all the natural number with each there's a corresponding irrational number, we can get a new irrational numbers by picking up the irrational on the diagonal of the existing list.

Because the new number is attained by picking the jth digit of the decimal on jth row, so it's different from any of the existing irrationals.
Therefore there are more irrational numbers than natural numbers, thus there are more irrational numbers than rationals.

Friday, November 26, 2010

A reflection on a wrong proof using induction.

Here is an counterexample which explains why the base case is so important for the proof.Sometimes it's hard to catch all the base cases which is required for continuing the induction part.

Statement:
f(x) = |x|: S $\rightarrow \!\,$ N, S is any set. f(x) is the cardinality of set S.
Try to prove: $\forall \!\,$ n $\in \!\,$ N, P(n) is true.
P(n) : $\forall \!\,$ S $\in \!\,$ {S| f(S)=n }, $\forall \!\,$
x, y $\in \!\,$ S $\Rightarrow \!\,$ f(x) = f(y).

Now is the wrong proof which causes a ridiculous conclusion:
Prove by induction:
Base case:
For n = 1, |S| =1 , S = {x}, $\forall \!\,$ x,y $\in \!\,$ S, x = y $\Rightarrow \!\,$ f(x) = f(y).
Induction:
Assume for n = k, $\forall \!\,$ S that |S| = k, P(k) is true,
   Then for $\forall \!\,$ x, y $\in \!\,$ S $\Rightarrow \!\,$ f(x) = f(y).
   Then fix |S| = k +1, Assume x, y, z $\in \!\,$ S. Let Sx = S\{x}, Sy = S\{y},
   Then |Sx| = |Sy| = k,
   Then for Sx, y and z $\in \!\,$ Sx,
   Then y = z     # According to the assumption for n = k
   Then for Sy, x and z $\in \!\,$ Sy,
   Then x = z     # According to the assumption for n = k
   Then x = z = y,
   Then x = y
   Then for n = k+1, P(n) is true,
   Then P(n = k) $\Rightarrow \!\,$ P(n = k+1)
Then for $\forall \!\,$ n $\in \!\,$ N,P(n) is true.

The proof above is wrong!
The reason is, the induction assume the k >= 3, which means the base case has to contain the case when n = 3 at least.Thus, we should include it in the base case that n = 1,2 ,3. The tricky part is starting from the case n =2, P(n) is no longer true,neither is the case n = 3. So the base case for this proof fails itself, that's the key point why the induction proof fails, and that's why we can draw such a ridiculous result that for any set of any cardinality, every element in the set is the same with any of the rest elements.

A reflection of this proof is , sometimes tricky thing may happen like the statement may be true for the induction part, but it can fail at the base case. that's why the base case and induction part are both very important.

Friday, November 19, 2010

Ordinary Induction Vs Complete Induction.

In math, the most frequently used induction proof is ordinary induction, but sometimes, complete induction requires stronger criteria,and thus more convincing. However, It is also proved that those two induction method can prove each other.

Ordinary Induction

Structure:

Let n be any number in Z+, p(n) be a statement satisfying the following two conditions.
(1) p(1) is true;
(2) For any k in Z+, p(k) is true then p(k+1) is true.

Then p(n) is true for all k in Z+.

2. An example of ordinary induction:

Question:Let P(n) be the statement "Postage of n cents (n>=12) can be formed using 4-cent and 5-cent stamps".

Proof:Base case: k = 12

P(12) is true, because 12 cents can be formed using three 4-cent stamps.

Induction:

Assume that P(k) is true, that is, that postage of k cents can be formed using some combination of 4-cent and 5-cent stamps.

Then to form postage of k + 1 cents, there are two possibilities.

1) If any 4-cent stamps were used to get k cents of postage, take one of the 4-cent stamps and replace it with a 5-cent stamp. You now have k + 1 cents of postage.

2) If only 5-cent stamps were used to get k cents of postage, since we know that k ≥ 12, we have at LEAST three 5-cent stamps. (I.e. the smallest k that can only be formed using 5-cent stamps is 15.) So if you replace any three 5-cent stamps with four 4-cent stamps, you will have k + 1 cents of postage.

Complete Induction:

Structure:

Let n be any number in Z+, p(n) be a statement satisfying the following two conditions.(1) p(1) is true;
(2) For any k in Z+, (p(1)^p(2)^...^p(k)) is true, then p(k+1) is true.
Then for k in Z+, p(n) is true.

2. An example of complete induction.
Same problem using complete induction:
Question:Let P(n) be the statement "Postage of n cents (n>=12)can be formed using 4-cent and 5-cent stamps".

Proof: Note that in order to show that p(n) is true for any n>=12 in N using complete induction, we need to show it's true for all the base case and also true for for n in N that 12<=n<=K, and then p(K+1) is also true. Then p(n) is true for any n>=12 in N.

Base case:

This proof requires 4 basis cases.

k = 12: 12 cents of postage can be formed using three 4-cent stamps.

k = 13: 13 cents of postage can be formed using two 4-cent stamps and a 5-cent stamp.

k = 14: 14 cents of postage can be formed using a 4-cent stamp and two 5-cent stamps.

k = 15: 15 cents of postage can be formed using three 5-cent stamps.

Induction:

For k > 15, assume that we can can form postages of j cents, for every j between 12 and k, inclusive (12 ≤ j ≤ k). Then, to form a postage for k + 1 cents, use the same postage as for k - 3 cents, but add a 4-cent stamp. Then for any j (12 ≤ j ≤ k), p(j) is true, then p(j+1) is also true. Then p(n) is true for any n>=12 in N.

Friday, November 12, 2010

Some tricky problems about the floor and ceiling of X

1.Definition of [x](Here I use the [x] for the floor of x.):

$\forall \!\,$ x $\in \!\,$ R, y = [x] $\Leftrightarrow \!\,$ y $\in \!\,$ Z and y <=x and $\forall \!\,$ z $\in \!\,$ Z, z <= x $\Rightarrow \!\,$ z <= y.

1.Prove: $\forall \!\,$ x $\in \!\,$ R, [x] > x - 1
Proof:
Assume x is a generic real number,
Then [x] $\in \!\,$ N,
Then [x] +1 $\in \!\,$ N,
Then [x] + 1 > [x]
Then [x] +1 > x # By contrapositive and according to the definition of [x]
Then [x] > x - 1.

2.Define a function: $\forall \!\,$ n in N, a(n) = [n/2]
Disprove: $\exists \!\,$ i $\in \!\,$ N, $\forall \!\,$ j $\in \!\,$ N, i < j $\Rightarrow \!\,$ a(i) = a(j).
Proof: To disprove this statement, we need to prove the negation of the statement is true.
That is: For any i in N, there exists a j in N, such that i < j and a(i) $\ne \!\,$ a(j).
Assume i is a generic natural number,
Pick j = i + 2,
Then a(j) = [j/2] = [(i+2)/2] = [i/2 + 1] = [i/2] +1
Then a(i) = [i/2]
Then a(i) $\ne \!\,$ a(j).
For any i in N, there exists a j in N, such that i < j and a(i) $\ne \!\,$ a(j).

Pay attention to two places:

1. About the definition of floor of x: [x], when using the second part of the definition, we have to make sure the z that is used for comparison is an integer.

Here we use the contra-positive of the second part of the definition, that is [x] if [x]+1 > [x], then [x] +1 > x.

(I made this mistake during the test2.!!!)

2. When we try to disprove some statement, we use the negation of the original statement, for the quantifiers we were using, we have to negate them and for the boolean, we need to make sure it follows:

negation of p $\Rightarrow \!\,$ q is (p and not q)

2.Now talking about the question about the ceiling of x(using [x] as well).

Definition:
$\forall \!\,$ x $\in \!\,$ R, y = [x] $\Leftrightarrow \!\,$ y $\in \!\,$ Z and y >=x and $\forall \!\,$ z $\in \!\,$ Z, z >= x $\Rightarrow \!\,$ z >= y.

Prove: for any x in R, [x] < x+1
Proof: Assume x is a generic real number,
              Then [x] < [x +1]
          Then [x] < x + 1      # According to the definition and contra-positive.
           Then for any x in R, [x] < x+1.

This is the same type of question which tests on the definition of ceiling of x.