Why is there more irrational numbers than rational numbers.

why are there far more real number than natural numbers? Why are there far more irrational numbers than rational numbers?
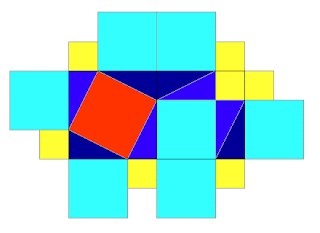
As shown in the graph above, it's called a consequence of the Pythagorean theorem: The length of the diagonal of a square is the square root of two times its side. The length of the square is a rational number while the length of diagonal is irrational. While we can just keep getting the 1/2 of the existing square to get infinitely many rational numbers, these natural numbers are countably many. But the number of irrationals are far more than the rationals, which is illustrated by the cardinality of the rationals and irrationals. |R\Q| >|Q|.
 
Now here is a trick to show why there are more irrationals than rationals.
We do this by trying to list all the real numbers in the interval (0,1).

First, because each of the rational numbers can be associated with a natural number by listing there like below.

In this way, each number is followed by its negative version, except zero, which doesn't have a different negative version. he fractions, if considered as improper fractions, are ordered by the sum of the numerator and denominator, starting with the fraction with the largest numerator: thus, we go through 4/1, 3/2, 2/3,1/5 in order. (Earlier, 2/2 was omitted, since that equals 1, which is already on the list.)
  N  Q
  1 1/1
  2 -1
  3 2/1
  4 -2/1
  5 1/2
  6 -1/2
  7  3
  8 -3
  9  1/3
  10 -1/3
  11 4
  12 -4

  ... ...

Then we can use all the natural numbers to list all the rational numbers. We have |Q| = |N|

Now we are trying to show there are more irrational number than rationals by trying to list all the irrationals by natural numbers.

.27231364585...
.40861132064...
.01678396536...
.81171944218...
.82122547689...
.17218943291...

...
We are trying to list all the real numbers by associating each with a natural number. But it seems there are always at least 1 more irrational number than all the rational numbers that we can list. Assume we listed all the natural number with each there's a corresponding irrational number, we can get a new irrational numbers by picking up the irrational on the diagonal of the existing list.

Because the new number is attained by picking the jth digit of the decimal on jth row, so it's different from any of the existing irrationals.
Therefore there are more irrational numbers than natural numbers, thus there are more irrational numbers than rationals.

A reflection on a wrong proof using induction.

Here is an counterexample which explains why the base case is so important for the proof.Sometimes it's hard to catch all the base cases which is required for continuing the induction part.

Statement:
f(x) = |x|: S N, S is any set. f(x) is the cardinality of set S.
Try to prove: n N, P(n) is true.
P(n) :  S {S| f(S)=n },
x, y S f(x) = f(y).

Now is the wrong proof which causes a ridiculous conclusion:
Prove by induction:
Base case:
For n = 1, |S| =1 , S = {x}, x,y S, x = y  f(x) = f(y).
Induction:
Assume for n = k, S that |S| = k, P(k) is true,
   Then for  x, y S f(x) = f(y).
   Then fix |S| = k +1, Assume x, y, z S. Let Sx = S\{x}, Sy = S\{y},
   Then |Sx| = |Sy| = k,
   Then for Sx, y and z Sx,
   Then y = z     # According to the assumption for n = k
   Then for Sy, x and z Sy,
   Then x = z     # According to the assumption for n = k
   Then x = z = y,
   Then x = y
   Then for n = k+1, P(n) is true,
   Then P(n = k) P(n = k+1)
Then for  n N,P(n) is true.

The  proof above is wrong!
The reason is, the induction assume the k >= 3, which means the base case has to contain the case when n = 3 at least.Thus, we should include it in the base case that n = 1,2 ,3. The tricky part is starting from the case n =2, P(n) is no longer true,neither is the case n = 3. So the base case for this proof fails itself, that's the key point why the induction proof fails, and that's why we can draw such a ridiculous result that for any set of any cardinality, every element in the set is the same with any of the rest elements.

A reflection of this proof is , sometimes tricky thing may happen like the statement may be true for the induction part, but it can fail at the base case. that's why the base case and induction part are both very important.

Ordinary Induction Vs Complete Induction.

In math, the most frequently used induction proof is ordinary induction, but sometimes, complete induction requires stronger criteria,and thus more convincing. However, It is also proved that those two induction method can prove each other.

• Ordinary Induction 

1. Structure: 

Let n be any number in Z+, p(n) be a statement satisfying the following two conditions.
(1) p(1) is true;
(2) For any k in Z+, p(k) is true then p(k+1) is true.

Then p(n) is true for all k in Z+.
 
   2.  An example of ordinary induction:

Question:Let P(n) be the statement "Postage of n cents (n>=12) can be formed using 4-cent and 5-cent stamps".

Proof:Base case: k = 12

P(12) is true, because 12 cents can be formed using three 4-cent stamps.

Induction:

Assume that P(k) is true, that is, that postage of k cents can be formed using some combination of 4-cent and 5-cent stamps.

Then to form postage of k + 1 cents, there are two possibilities.

1) If any 4-cent stamps were used to get k cents of postage, take one of the 4-cent stamps and replace it with a 5-cent stamp. You now have k + 1 cents of postage.

2) If only 5-cent stamps were used to get k cents of postage, since we know that k ≥ 12, we have at LEAST three 5-cent stamps. (I.e. the smallest k that can only be formed using 5-cent stamps is 15.) So if you replace any three 5-cent stamps with four 4-cent stamps, you will have k + 1 cents of postage.

• Complete Induction:

1. Structure:

Let n be any number in Z+, p(n) be a statement satisfying the following two conditions.(1) p(1) is true;
(2) For any k in Z+, (p(1)^p(2)^...^p(k)) is true, then p(k+1) is true.
Then for k in Z+, p(n) is true.

   2. An example of complete induction.
Same problem using complete induction:
Question:Let P(n) be the statement "Postage of n cents (n>=12)can be formed using 4-cent and 5-cent stamps".

Proof: Note that in order to show that p(n) is true for any n>=12 in N using complete induction, we need to show it's true for all the base case and also true for for n in N that 12<=n<=K, and then p(K+1) is also true. Then p(n) is true for any n>=12 in N.

Base case:

This proof requires 4 basis cases.

k = 12: 12 cents of postage can be formed using three 4-cent stamps.

k = 13: 13 cents of postage can be formed using two 4-cent stamps and a 5-cent stamp.

k = 14: 14 cents of postage can be formed using a 4-cent stamp and two 5-cent stamps.

k = 15: 15 cents of postage can be formed using three 5-cent stamps.

Induction:

For k > 15, assume that we can can form postages of j cents, for every j between 12 and k, inclusive (12 ≤ j ≤ k). Then, to form a postage for k + 1 cents, use the same postage as for k - 3 cents, but add a 4-cent stamp. Then for any j (12 ≤ j ≤ k), p(j) is true, then p(j+1) is also true. Then p(n) is true for any n>=12 in N.

Some tricky problems about the floor and ceiling of X

1.Definition of [x](Here I use the [x] for the floor of x.):

x R, y = [x] y  Z and y <=x and z Z, z <= x z <= y.

1.Prove: x R, [x] > x - 1
Proof:
Assume x is a generic real number,
Then [x] N, 
Then [x] +1 N,
Then [x] + 1 > [x]
Then [x] +1 > x    # By contrapositive and according to the definition of [x]
Then [x] > x - 1.

2.Define a function: n in N, a(n) = [n/2]
Disprove: i N, j N, i < j a(i) = a(j).
Proof: To disprove this statement, we need to prove the negation of the statement is true.
That is: For any i in N, there exists a j in N, such that i < j and a(i) a(j).
Assume i is a generic natural number,
Pick j = i + 2,
Then a(j) = [j/2] = [(i+2)/2] = [i/2 + 1] = [i/2] +1
Then a(i) = [i/2]
Then a(i) a(j).
For any i in N, there exists a j in N, such that i < j and a(i) a(j).

Pay attention to two places:

1. About the definition of floor  of x: [x], when using the second part of the definition, we have to make sure the z that is used for comparison is an integer.

Here we use the contra-positive of the second part of the definition, that is [x] if [x]+1 > [x], then [x] +1 > x.

(I made this mistake during the test2.!!!)

2. When we try to disprove some statement, we use the negation of the original statement, for the quantifiers we were using, we have to negate them and for the boolean, we need to make sure it follows:

negation of p q is (p and not q)


2.Now talking about the question about the ceiling of x(using [x] as well).
 

Definition:
x R, y = [x] y  Z and y >=x and z Z, z >= x z >= y.

Prove: for any x in R, [x] < x+1
Proof: Assume x is a generic real number,
              Then [x] < [x +1]
            Then [x] < x + 1      # According to the definition and contra-positive.
           Then for any x in R, [x] < x+1.

This is the same type of question which tests on the definition of ceiling of x.